Isolated $\mathscr{B}$lack Hole Horizons

Introduction

A Black Hole is a collection of events that is causally disconnected from observers in the asymptotic future, studied as a subset of the geometrical 4-dimensional spacetime manifold. It is defined by the enigmatic Event Horizon, which serves as a boundary beyond which no future-directed causal signal from inside the region reaches distant observers. Historically, black holes have been extensively studied through global methods by exploiting the mathematical richness of topology with causality. The interplay between topology and local causality yields striking results, most notably the uniqueness theorems [1,2] and their analogies with thermodynamics via the laws of black hole mechanics.

However, the conventional characterization of black holes through event horizons, which is rooted in topology, encounters a teleological issue with non-locality. Defining the causal past requires knowledge extending to infinity from which we work our way backward, which complicates both practical applications and conceptual understanding.

A paradigm shift is through quasi-local definitions, specifically isolated and dynamical horizons [3,4,5]. By promoting the concept of a quasi-local isolated horizon and using its intrinsic geometry as initial data, it becomes possible to integrate the Einstein equations outward.

Preliminaries

The richness of the causal structure of spacetime is enlightened through the Newman-Penrose (NP) formalism [6,7], which establishes a spinorial null basis for General Relativity (GR), revealing the symmetries of spacetime. This is a tetrad formalism that uses an orthonormal basis to define the local spacetime, analogous to that of special relativity. Special relativity is typically characterized using Minkowski coordinates in a Galilean frame of reference, which involves separating the physical spacetime into unphysical space and time through an arbitrary foliation. However, the NP tetrad is defined using a basis composed of four null vectors, of which only three are linearly independent, which reveals the spinorial structure of hyperbolic spacetime in special relativity. These vectors are specifically adapted to light geodesics, which are physically significant as they determine the conformal structure of spacetime, and therefore causality.

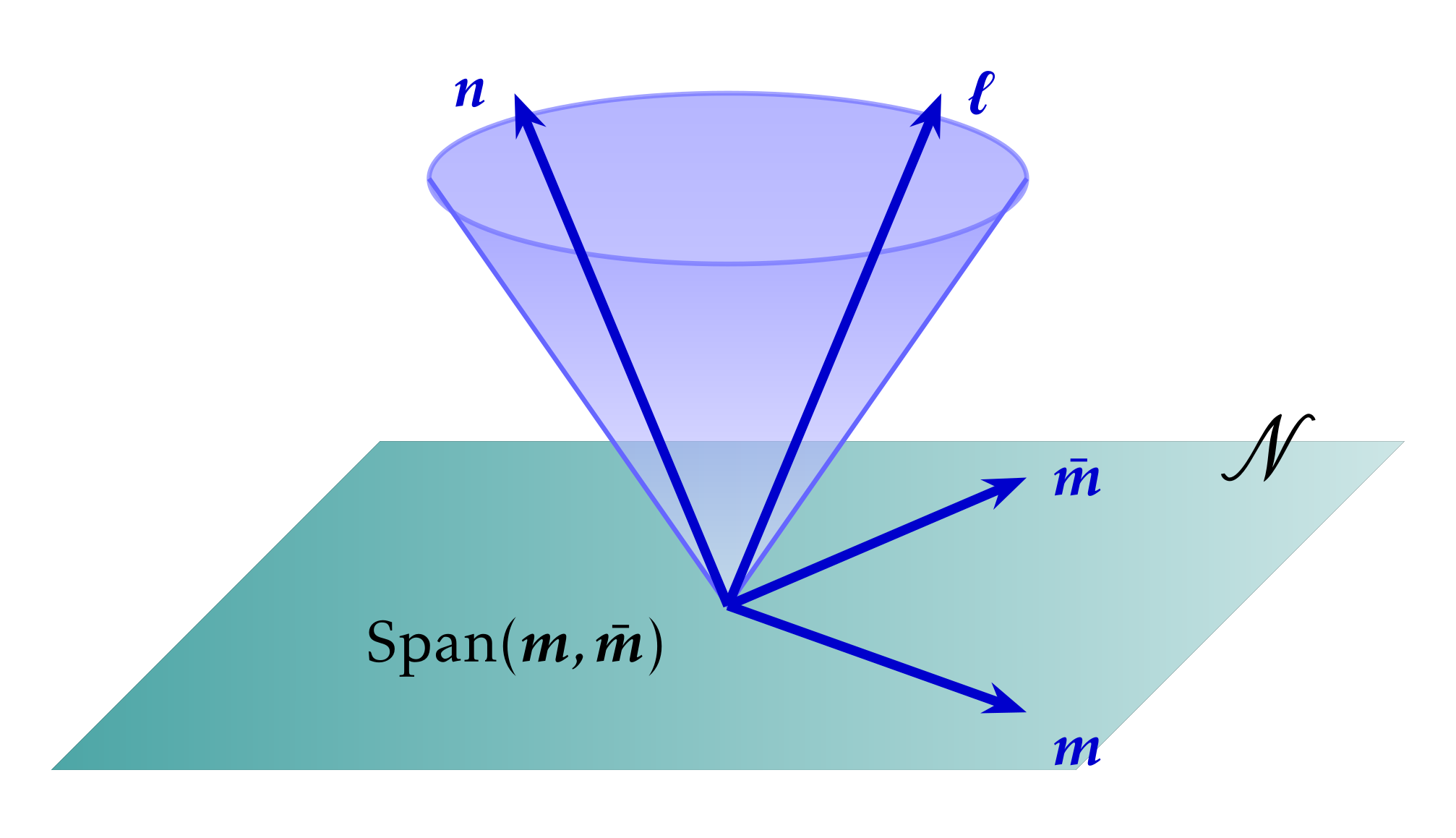
The light cone structure of the spacetime of the black hole solutions of GR makes the NP formalism effective for grasping the inherent symmetries of these spacetimes and revealing their analytic richness. We choose the null basis tetrad, consisting of real null vectors, $\boldsymbol{\ell}$ and $\boldsymbol{n}$, and complex conjugates $\boldsymbol{m},\bar{\boldsymbol{m}}$, with the orthonormal relations, $\boldsymbol{\ell\cdot m}=\boldsymbol{\ell\cdot \bar{m}}=\boldsymbol{n\cdot m}=\boldsymbol{n\cdot\bar{m}}=0$. We further introduce the following normalization conditions on the basis vectors as $\boldsymbol{\ell\cdot n}=1$, and $\boldsymbol{m\cdot \bar{m}}=-1$, such that the spacetime metric $\boldsymbol{g}$ can be written in terms of the complete basis as, $\boldsymbol{g}=-\boldsymbol{\ell}\otimes\boldsymbol{n}-\boldsymbol{n}\otimes\boldsymbol{l}+\boldsymbol{m}\otimes\boldsymbol{\bar{m}}+\boldsymbol{\bar{m}}\otimes\boldsymbol{m}.$

The nature of the tetrad vectors is primarily encoded in the spin coefficients for directional derivatives along the basis vectors, which constitute the antisymmetric connection. This antisymmetry profoundly manifests the power of the tetrad formalism in representing the curvature through fewer independent components, and is described by the NP field equations. The curvature components are projected onto the relevant Ricci and Weyl scalars, which exhibit spinorial symmetries and are constrained by the Bianchi identities.

Isolated Horizons

It is customary to model horizons by globally stationary solutions, but physically one needs only quasi-local boundary conditions that make the horizon isolated: the horizon’s intrinsic geometry is time-independent while the exterior may be radiative. In practice, this is enforced by conditions on the null generators rather than by global stationarity.

We build up to the idea of isolated horizons (IH), by first understanding non-expanding horizons (NEHs), which are null hypersurfaces having a vanishing expansion along any null normal, which further induces an affine connection on the null horizon uniquely. We proceed to restrict the rotational scalar defined through the induced connection to remain constant on the horizon, to obtain a weakly isolated horizon (WIH). The intrinsic geometry of the IH is more restrictive than that of a WIH, and strengthens the notion of isolation by requiring the intrinsic metric and the full derivative operator to be time independent, thus constant on the horizon. The laws of black hole mechanics, initially proved for event horizons, are generalized to IHs.

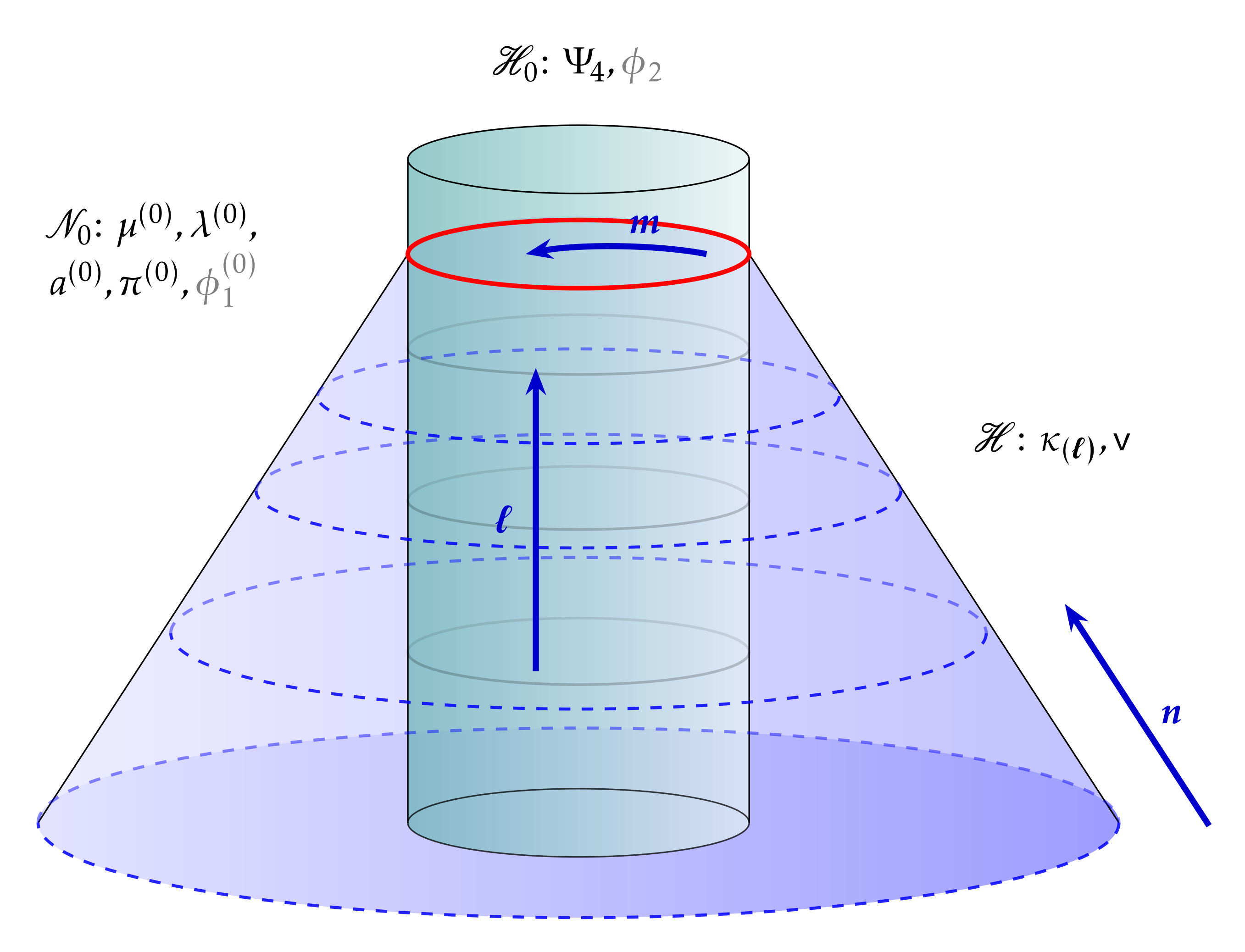
Probing Near-Horizon Structure

The construction of the near-horizon geometry follows by prescribing initial data on transverse null hypersurfaces and using the Einstein equations to obtain the spacetime metric in a neighborhood. For studying the geometry and specifying initial data, we apply the Characteristic Initial Value formulation [8,9], and further foliate the horizon, $\mathscr{H}_0$, into submanifolds which are spacelike, characterized as the cross sections, $\mathscr{N}$.

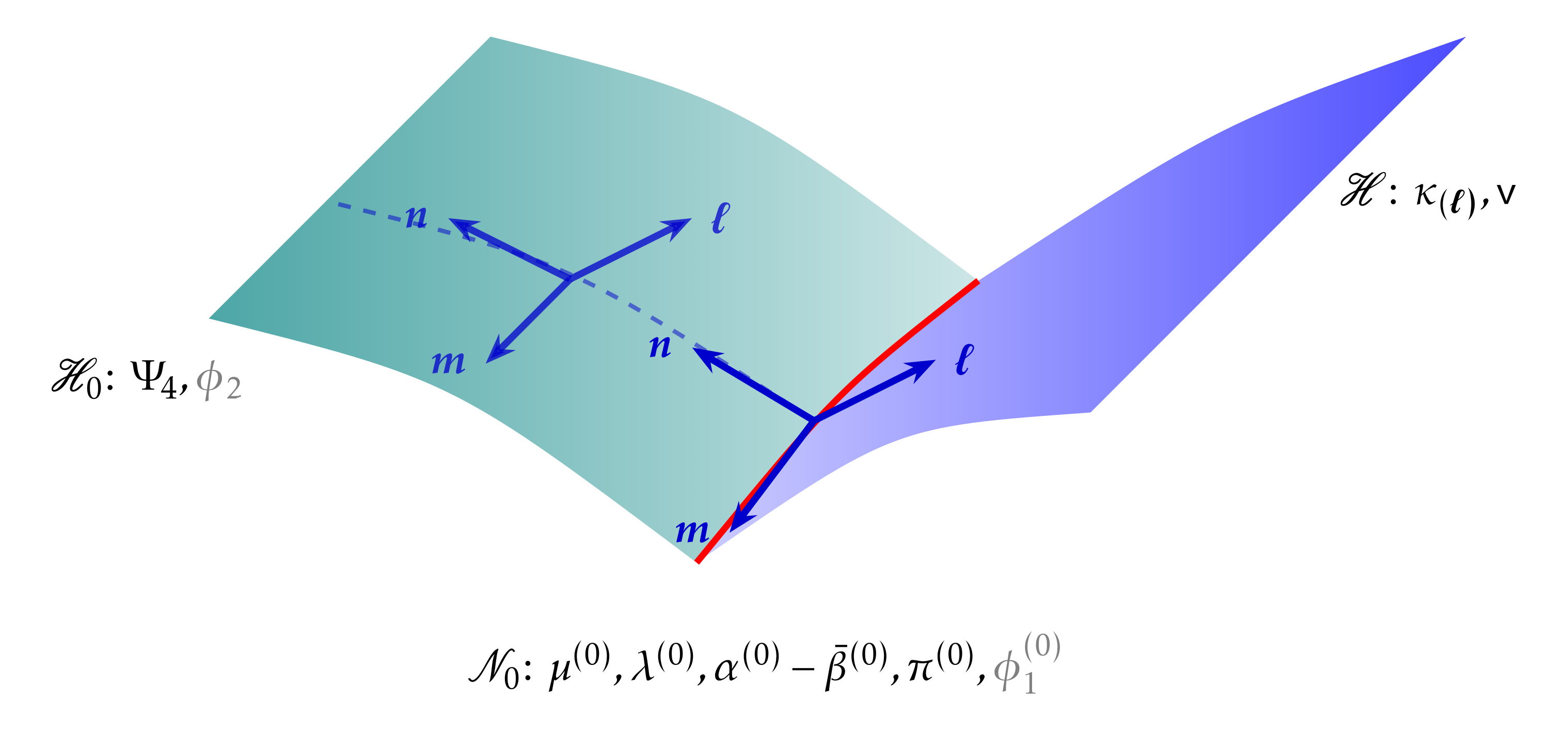
All aspects of the classical IH formalism are essential in building the near-horizon geometry. Firstly, the Hamiltonian calculations provide us with appropriate values for mass and surface gravity for the spacetime. Secondly, the geometric constraints on the IH needed to be satisfied in accordance with the algebraic properties of the Weyl tensor. Thirdly, the multipole moments yielded the intrinsic geometry and curvature. Lastly, the radial and angular NP field equations provide us with extensions of the local definitions across the spacetime.

We examine the intrinsic geometry of the null surface $\mathscr{H}_0$, which is foliated temporally, defined by the tangent vector $\boldsymbol{\ell}$. We radially integrate on the past null cone $\mathscr{H}$, generated by past-directed null geodesics originating from a cross-section $\mathscr{N}_0$. Thereby, the spacetime metric is constructed starting with suitable data on $\mathscr{H}_0$, $\mathscr{H}$, and $\mathscr{N}_0$.

Tidal Deformabilities

In the presence of a tidal environment, a black hole can be influenced by an external gravitational field generated by nearby objects or by scalar or vector fields. Love numbers quantify how an object responds to tidal forces: if the external tidal field behaves like $\mathsf{r}^{\ell}$ at a large distance $\mathsf{r}$, where $\ell$ represents the relevant multipole moment, an object like a star that experiences tidal deformation will generate a response field that decays as $1/\mathsf{r}^{\ell+1}$ at large distances. The coefficient of this decay, normalized by the amplitude of the tidal field, is referred to as a Love number for the multipole. Analogous to gravitational Love numbers, we can define surficial Love numbers as the deformation of the body’s surface, also expanded in multipole moments.

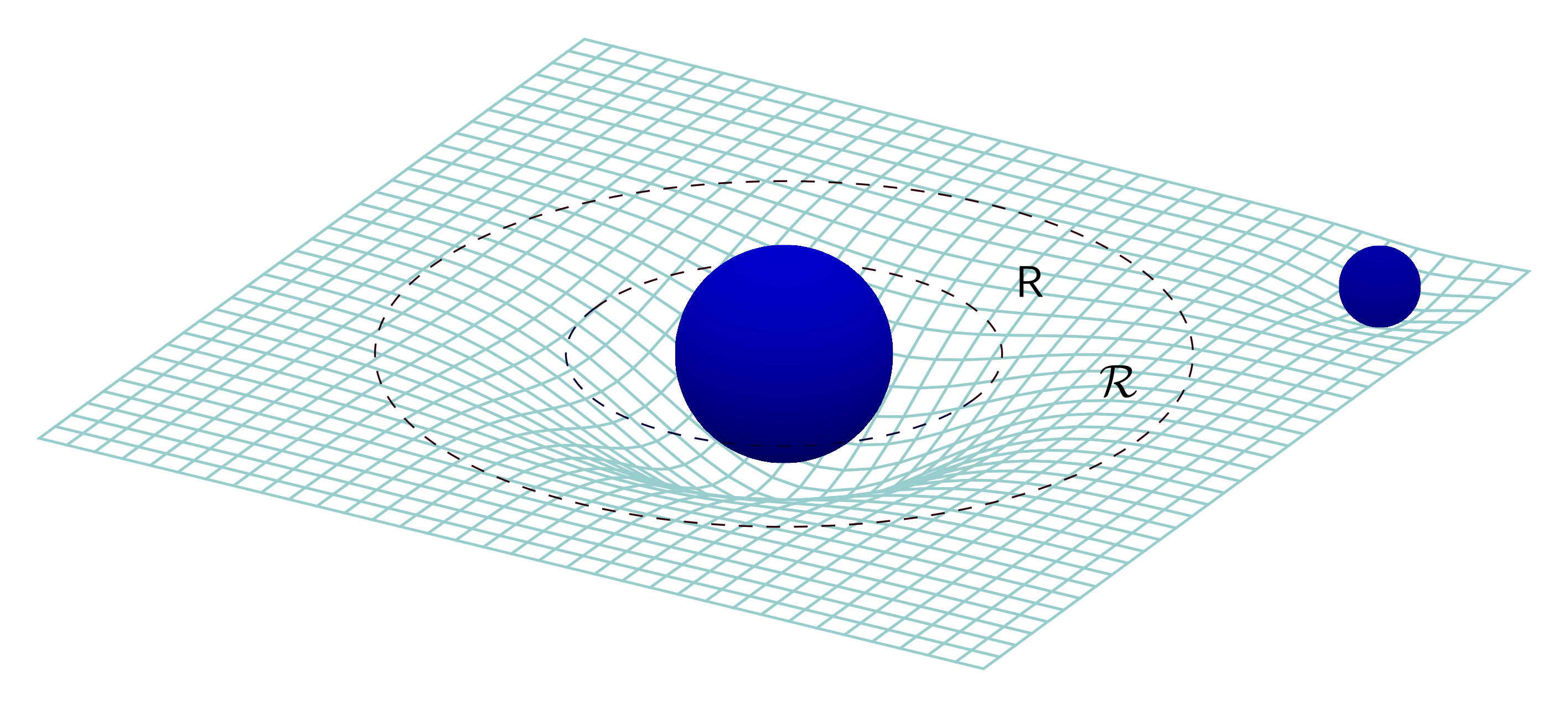
For a weak static tidal field, the problem reduces to studying static linear perturbations [10] around the object of interest. At leading order, tidally perturbed black hole horizons can be modeled as IHs, and the non-vanishing fluxes of infalling radiation can be calculated at linear order using perturbation theory.